Mathematics and Design for Young Children

Here you’ll find methods for developing in 3- to 5-year-old children a sense of competence and enjoyment in exploring cognitive-mathematical activities. Mathematics for this age group is more than numbers: it includes writing symbols, creating designs, counting stuff, the comprehension of number, sequencing, ordering, patterning, beginning graphing, problem solving, and discovering how clever they are in reframing experience through the affordances of logical-mathematical thinking.

Since math is academic, like reading, huge external pressure is put upon teachers to teach it; they HAVE to teach it or children won’t learn it—even to children as young as two! Despite the (1) clear evidence that math education fails up to half of all children, youth, and adults, and (2) the growing army of voices who strongly shout, “Children would do better having a childhood playing and discovering what interests them, including, by the way, number.” Research and sense apparently have no say in school policy; the pressure remains constant; the marketing of useless materials is rampant.

Including books. There are soooooo many books on math for children and meaningless articles online. It’s easy to find lessons and worksheets all ready to go. It’s STEM, after all, the inside track to success in life. Buy this! It’s attractive to children; it’s got red, yellow and blue!

You might be thinking “Why would I be interested in Tom’s huge bunch of pages on math for kids?” 

You are now here at a doorway to math and design as a natural language. Young children learn it just as they learn to run and draw: they enjoy it.

An Invitation

I invite you to walk through the door and see what you find. I am offering a course here with the specific ways for children to find mathematics to be a natural part of life. Children become intrigued with the language of mathematics because the stage is set for them to take the initiative and become engaged with others who are engaged, too.

If you would like to find out how this works, I invite you to at least read a few paragraphs more before you click away—say, down the page to just beyond the snowball picture.

I’d like to show you what it is like to build curriculum to educate young children in academic content. After my not too windy example, I will ask you a question: Is this teaching?

Ahead are unique resources like these

Counting Cards With PDF Counting Cards Without PDF
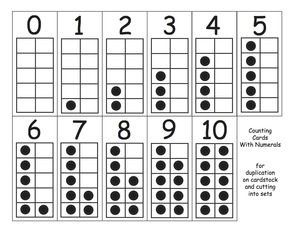
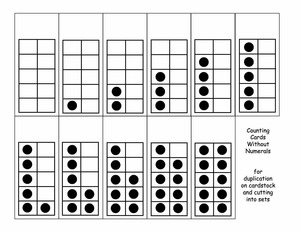Based on the work of Friedrich Fröbel, you can find a way of commenting to children who arrange shells on black felt because what they do is so amazingly cool.

And fun games to do with children,

Many of us may Be Abuse Survivors

For many educators math has never been much fun. Most of the students in my Math for Young Children classes raised their hands in agreement with the statement, “I’m no good at math.”  (Many fewer agree with “I’m no good at reading.” What does that say?)

Could there be a fun way for both educators and children to be excited about mathematics? Yes, there is. Really fun.

Instead of the dread, here you will find…

… an absolutely natural mathematics curriculum—as natural to children as running and jumping. The linked pages—with deeper levels beyond what you see in the menu—become an entire college course on becoming the leader of a community of young children learning through their playful engagement.

• You will find a way to offer mathematics and design experiences to young children in free play, in small group settings, and in the full class group.
• You also will find challenges to your own expectations about what kinds of math one is looking for as children explore and discover together.
• You will find how to create a classroom culture that starts slowly at first and then gathers speed, like a snowball rolling downhill. The energy is amazing. A child’s peers are the gravity rolling the snow balls downhill according to the forces of nature, drawing interest in noticing and figuring out stuff.
• You will find a structure that engages young children in the language of mathematics, which offers ways of reconceptualizing simple life events, like the shoes in the hall, in a surprising way. That noticing becomes a game of further noticing, leading onward into representations and abstract relationships.

Math is Language

It took me some years before I began to understand how mathematics for young children operates as a way to communicate in another language. We learn to use a language, like theater, blocks, or clay, because we encounter understandings and attend to experience differently. Mathematics is a way of thinking with its own discoveries, connections, and possibilities in a continuing maze of doorways to further understandings and awarenesses. For young children the key is to find how fun it is to explore ways to think anew about common experiences.

Four Blocks

I’d like to present an example of what I am driving at using this image of a child’s hand on a blue table with four flat blocks.

I don’t know any more than you do about what’s going on, but we do have facts upon which we can have a discussion. (1)This is a photo someone took and shared with me. (2)The photo shows a table, a child in a chair, and four 1″x3″ wooden blocks. (3)Three of the blocks are aligned parallel forming a square and one block is butted against the ends, at right angles, slightly ajar.

I think we could agree on a few things about those facts. I think most people would be comfortable assuming this child intentionally placed them this way. Further, we could also conclude from the placement of the child’s hand that the child paused to have the arrangement photographed.

Building upon those projected meanings, we could assume pausing and photographing was normal in this particular setting. The child’s face isn’t included in the shot, which we could assume further that this moment was about the block arrangement rather than a photo about the child. Taking that one step farther, maybe the child expected, at times, that someone might stop, notice, comment, and even photograph their work. These are all meanings that have a reality because we agree, at least in terms of this discussion, that they are reasonable conclusions.

Imagine, then, what might result next if you and your group of colleagues shared your own opinions of what might be going on for this child, whom you know, whose hand you see. Your thoughtful group might share your best guess not only about the child’s intention but also about the child’s aesthetic sensibility. Because you all get to discuss it, you could agree that this arrangement conveys information not only about number but also about beauty. The arrangement itself communicates much more than what one can easily say in words. That’s blocks as a language.

This changes everything

If you want to read these flat wooden blocks as an expression containing number, your community could treat them as manifestations of how four-ness works. Four has consistency no matter what the arrangement. That constant, if recognized rapidly, without the need to count, is an understanding in arithmetic called subitizing. Another basic concept, partitions, is represented as one-three, which could be expressed in English as “one plus three” or expressed in symbols as 1+3 or 4-1 or 4/3 or 3/4 or 1/4 or 3:1 or 25% and 75%.

If you want to read these flat blocks as a story, too, it could be the wolf attacking the house of three little pigs.

If you want to read these blocks as something of beauty, you could appreciate the child’s arrangement of wood grain, perhaps, flowing across the faces.

The point I am making is that points of view alter how one regards the possibilities present.

Simple events can surprise us with their breadth of possibilities, which alters not only our adult perspectives but also the doors that now open for altered inventiveness in the children’s future. Imagine that talking like we did above might change how this child places blocks in free play, to make a unicorn corral perhaps. Imagine further that this child is playing with others who have heard talk of beauty or partitions, too.

If so, it is not too difficult to imagine that they might be likely to talk about their intentions as they built that corral together, say with wood grain aligned or fence sections in threes. The multiple perspectives of one-three block arrangement, the three little pigs story, and the beauty of the knots in the wood are noticeable to them. We can imagine the synergy being released in their resonant interest (The Stewardship of Play) to fuel further inventions and expressions, leading upward (The Learning Frame).

All the while the children remain free, in play, to discover who they are. We don’t have adults messing things up by “teaching.” It’s a different kind of school.

Imagine this school:

1. The educators offer elegant, aesthetic materials with mathematical affordances.
2. A child happens to arrange four of them as above and pause.
3. The educator notices the arrangement, because she was looking for it, and comments using any of the mathematical, aesthetic, or story attributes she thinks might intrigue this child at this moment.
4. The educator takes a photograph that records this event. She prints it to stick on the wall near that table, which the children might notice tomorrow. She emails the image home for the family and the child to discuss if they want. She shows it to the whole group of children because she is interested in what discussion might take place. She is most eager to show to her workmates, because she values the different perceptions of its meaning and what possibilities could be invented.
5. The child, whose impulse arranged them this way, gets to reconsider that event through the lens of what it conveys, which in turn may raise thoughts of other experiences she has had. In whatever way she found interesting, mathematics or design, she takes forward into her life an expanded noticing and altered intentions.
6. A child across the table looks at the child being noticed, sees the camera emerge, and hears the comments. He may offer a comment, too, or reconsider his own materials in a new light.

One event of initiative, engagement and intentionality—commented upon, recorded, and shared with the community—becomes a model of discovery not only supporting the inventiveness of this one child but also marking this community of children as the clever beings they are. Being tricky, after all, is what we do at school.

Building a Relational Culture

An event when captured and reviewed from a mathematical and design perspective stimulates connections to pattern, symbols, sequences, and so on, changing expectations in approaching a pile of plain old wood blocks. Relational spaces make connections more likely among the children. I use a special time of the day, which I call workstations, adding energy to the mathematic discoveries. In group times I offer simple demonstrations, like counting visible buttons on clothes or graphing flavors of ice cream or playing The Hand Game. Since all the children know the games from those shared times, they bring attentiveness to mathematics in their play, enabling freer communication and cooperation among children, connecting with others who may not necessarily be best friends. These integrated free times and group times build the culture of the school.

Is this teaching?

Returning to the image of the four blocks and the numbered list of events above, would you say the educators in this setting taught mathematics?

I wouldn’t. I would say the educator had clear intentions in what she was looking for, intention to be present and to listen at the right moment, and intention in having her camera ready. Clever-as-a-fox leadership capitalized on a small event to build a culture-of-clever in the classroom. Of course, behind it all, was an intentionality of allocating time, sourcing particular kinds of materials, and building the physical spaces where children could see each other work. Would you call that teaching mathematics?

I appreciate you taking the time to read this far. You now can see how difficult it is to convey these ideas to others.

Academic Expectations

Gotta get ’em ready for kindergarten? Have to show “readiness” in your work? This is a sham, a diversion from not passing laws that provide resources for early education and care for all children with family support wages. Readiness? How can one be ready for significant change? Were you ready for marriage? Ready for a baby? Ready for high school? Ready for graduation? What is ready?

If a reasonable person looked at the broad diversity of children, the inescapable fact, that the research both confirms and obscures, is that it is impossible to determine a “readiness point” for an imagined future. Generalizations do not hold up. Picking a standardized readiness point always furthers racism, cultural bias, and current structures of privilege. People with power over other people, the ones choosing, play games with certainty.

Readiness is an imagined goal with ghost goalposts, which only has a negative effect on children: the rationale for an assessment is to find children who are lacking something. We don’t know why, really, but we pretend that finding an inadequate pile does nothing for children, but it does draw resources away that could be invested elsewhere. It defies the first ethical test: First, do no harm.

Readiness hasn’t been attacked enough. I have watched children of many abilities (and unfortunate adversities) lovingly and richly grow, each in their unique ways, into powerful, capable, and generative human beings when they are treated well, fed, listened to, and valued. We know what matters is not an artifice; what matters are the children you see in front of you and can help; you want to see them engaged and laughing. We all children deserve to participate in a community of generative energy and joy.

We know it’s pretty cool what young children do with their naturally curious brains when they have chance and opportunity to discover, with others, how the world works. We could discard the search for math skills rationalized as readiness for Kindergarten and demand something more lasting and beneficent.

Goal for Mathematics and Design

We want children to develop effective habits of mind (wondering, figuring it out, predicting, and challenge-seeking) and the disposition to participate in cooperative inquiry for extended periods of time.

(Not stuff like “counts how many to twenty and beyond” which is one example in our state’s Learning Pathways to Counting and Cardinality.)

Deep Understandings About Learning Math

If you want to see how this is done and even be able to do it with little time and few resources, I recommend you first invest in yourself by taking on the challenges presented in the slide show below. It is worth it because you can see and experience something that you can’t really convey in words.

It is a sequence of hands-on explorations for adults borrowed from Marilyn Burns. If you participate you will explore predicting length and volume. Please do this with a partner, because alone you miss the point. Understanding what happens with others is essential to a healthy facilitation of experiences in mathematics for young children. Because you construct these deep understandings yourself, you’ll never forget them. If you do this, you will be in a place where you wish others understood, too: telling them doesn’t work.

To do the activities you will need some materials ready.

These experiments are ideally undertaken in pairs or trios, so each person contributes to the discussion and the group can discover how interaction with others becomes essential to the encounter. The picture below lists what you and a partner have to gather to do the experiments.

Once you have the equipment, you can click play.

After you have done the activity, you can peek at what others before you thought at this link. Experiment Reflections

Ahead:

Arithmetic Skills

Arithmetic — one aspect of mathematics — includes, at this age, counting, quantity, and the basic symbols. These acquisitions can be classified as skills (practiced abilities), concepts (mental understandings that are constructed over time), and making connections to symbols once those understandings are strong. Included in the Arithmetic Skills portion is a discussion of assessment, something I have found essential to address. The goal here is to be able to see the skills and concepts as they emerge and communicate that to families.

Independent Activities

The heart of this work is the creation of a time for children to inquire, discover, and practice what they are interested in individually and cooperatively. Having the children engaged allows educators the opportunity to document in order to reflect upon the children’s work and begin to build the culture of inquiry. Independent means free. Adults listen, watch, and respond — and hopefully never ask another question! In this section are videos of children at work, pages that offer ways you might construct a similar space, and how to respond to children’s work. Both Fröbel and Malaguzzi figure big in this discussion.

Group Games

Educators can lead brief games and challenges, both formal and informal, that create a community of children who are excited to experience their mathematic brains. This is not free play time; it’s a routine gathering or something to do while in a group waiting for the bus. Since the children all have these same experiences, they bring a shared background into their independent activity time. I have had so much fun leading these.